基于单神经元的PID控制

1 神经元

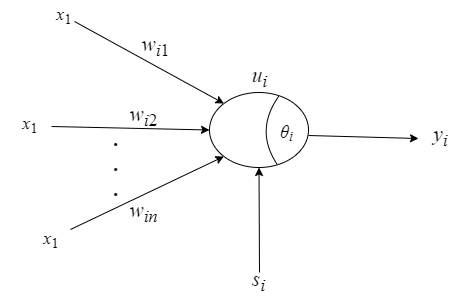
​ 单神经元作为构成神经网络的基本单位，具有自学习和自适应能力，且结构简单响应速 度快。这里将单个神经元与传统 PID 控制器结合起来，一定程度上解决了传统 PID 调节器不易在线实时整定参数，难以对复杂过程和时变系统参数进行有效控制等问题。人工神经元模型如图1所示，可以看出神经元是一个多输入单输出且具有阈值、权值的非线性处理元件。神经元突触可与其他神经元相连接，或反映外界环境信息，也可以反馈自身信息，通过调整权值得到新的输出。 $$ net_i = \sum_jw_{ij}x_j +s_j - \theta_i \ u_i = f(net_i) $$

图1.1 人工神经元模型

2 单神经元 PID 控制

2.1 单神经元 PID控制器的设计

​ 用单个神经元实现的自适应 PID 控制的结构框图如图2.1所示。

图2.1 单神经元自适应 PID 控制的结构框图

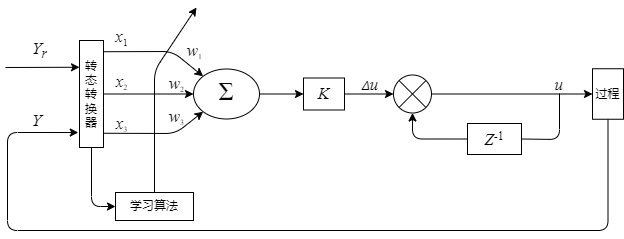
​ 图中$Y_r$为设定值，$Y$为给定值，通过状态转换器得到$x_i (t)(i = 1,2,3) $作为神经元输入的三个状态量，通过学习调节神经元权值 $w_i(t)(i = 1,2,3)$最终得到输出。神经元的输入输出关系描述为: $$ I = \sum_{i=1}^{3}w_ix_i ......(2.1) \ y = f(I)..........(2.2) $$ ​ 由PID控制器的增量算式$\Delta u = K_P[e(k)-e(k-1)]+K_ie(k)+K_D[e(k)-2e(k-1)+e(k-1)]...(2.3)$，若取$X_1 = e(k)-e(k-1), X_2 = e(k), X_3 = e(k)-2e(k-1)+e(k-1)$，则式变为$\Delta u = w_1[e(k)-e(k-1)]+w_2e(k)+W_3[e(k)-2e(k-1)+e(k-1)]...(2.3)$，比较式(2-3) 和(2-4) 形式完全相同，所不同的只是式(2-4) 中的系数$w_i(t)(t=1,2,3)$，可以通过神经元的自学习功能来进行自适应调整，而式(2-3) 中的参数$K_P, K_I, K_D$是预先确定好且不变的。正是由于$w_i$能进行自适应调整，故可大大提高控制器的鲁棒性能。

​ 与常规PID控制器相比较，无需进行精确的系统建模，对具有不确定性因素的系统，其控制品质明显优于常规PID控制器。从后面的仿真分析中可以验证这一结论。其中，神经元的学习功能是通过改变权系数$w_i$来实现的，学习算法即是如何调整$w_i$规则，它是神经元控制的核心，反映了学习方式与学习功能。神经网络的工作过程主要由两个阶段组成，一个阶段是工作期，此时，各连接权值固定，计算单元的状态变化，以求达到稳定状态。另一个阶段是学习期，此时可以对连接权值进行修改。

2.2神经元 PID 学习算法

​ 神经元的学习功能是通过改变权系数$w$来实现的，学习算法即是如何调整$w$的规则，它是神经元控制器的核心，反映了学习方式和学习能力。如何调整$w$对整个控制系统抗干 扰能力和自适应性能都有很大的影响。 权值$w_i(k)$的修改学习规则如下: $$ \left{
\begin{array}{lr}
w_1(k+1) = w_1(k) + \eta_Pu(k)e(k)x_1(k), & \
w_2(k+1) = w_2(k) + \eta_Iu(k)e(k)x_2(k), \
w_3(k+1) = w_3(k) + \eta_Du(k)e(k)x_3(k), &
\end{array}
\right. $$ ​ 为了保证学习算法的收敛性和控制的鲁棒性，对上述算法进行规范化处理后可得如下的 算法： $$ \left{
\begin{array}{lr}
\Delta u(k) = K\sum_{i}^{3}w_i^{'}(k)x_i(k), & \
w_i^{'}(k) =\frac{w_i(k)}{\sum_{i}^{3}w_i(k)}, \
w_1(k+1) = w_1(k) + \eta_Pu(k)e(k)x_1(k), & \
w_2(k+1) = w_2(k) + \eta_Iu(k)e(k)x_2(k), \
w_3(k+1) = w_3(k) + \eta_Du(k)e(k)x_3(k)
\end{array}
\right. $$ 其中，$\eta_P,\eta_I,\eta_D$分别为比例、微分、积分的学习速率，$K$为神经元的比例系数$K>0$。

这里参数选取的一般规则如下：

​ ① $K$是系统最敏感的参数。$K$值的变化，相当于$\eta_P,\eta_I,\eta_D$三项同时变化，因此$K$值

的选择非常重要，应在第一步先调整$K$。$K$越大，则快速性越好，但超调量大，甚至可能

使系统不稳定。当被控对象时延增大时，$K$值必须减少，以保证系统稳定。$K$值选的过小，

会使系统的快速性变差。然后根据“② ⑤”项调整规则调整 $\eta_P,\eta_I,\eta_D$。

​ ②对于阶跃输入，若被控对象产生多次正弦衰减现象，应减少$\eta_P$，其他参数不变。

​ ③若被控对象响应特性出现上升时间短、超调过大现象，应减少$\eta_I$，其他参数不变。

​ ④若被控对象上升时间长，增大$\eta_I$又导致超调过大，可适当增加$\eta_P$，其他参数不变。

​ ⑤在开始调整时，$\eta_D$选择较小值，当调整$\eta_I$和 $\eta_P$，使被控对象具有良好特性时，再逐渐增大$\eta_D$，而其他参数不变，使系统输出基本无波纹。

2.3 实验验证

​ 对输入信号为阶跃信号，采样时间为1ms，被控对象为 $$ G_p(s) = \frac{133}{s^2+25s} $$ 编写并运行程序，经过调试，得到以下图像。

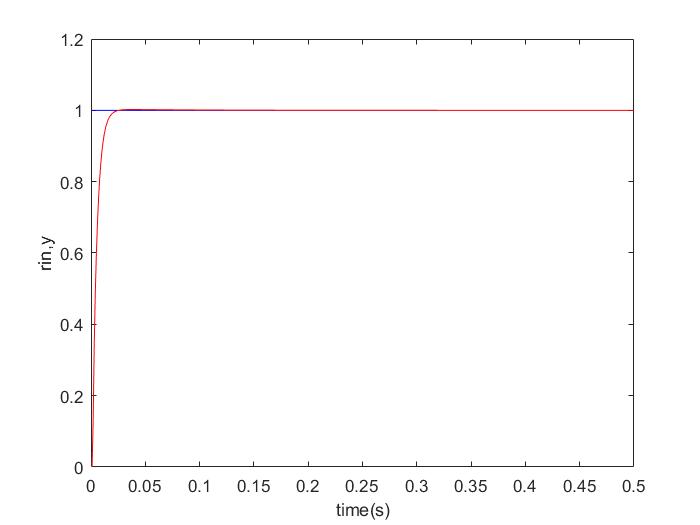
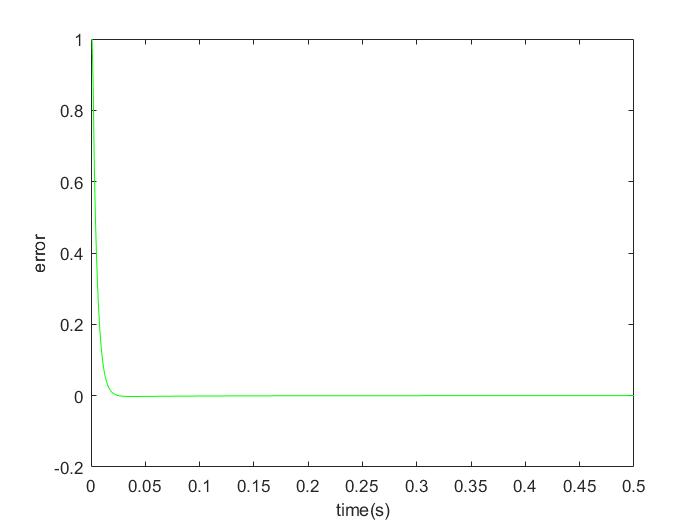
附件 - 源码

%Single Neural Adaptive PID Controller 
clear all; 
close all; 

ts = 0.001;

%离散化系统
sys=tf(133,[1,25,0]); 
dsys=c2d(sys,ts,'z');
[num,den]=tfdata(dsys,'v');

%初始化
x=[0,0,0]'; 

%------------------第一套系数--------------------------%
%初始化学习率
xiteP=4.0;      %第65行用到
xiteI=0.09;     %66
xiteD=1.1;      %67

%神经元的比例系数
K=2000;         %80

%------------------第二套系数--------------------------% 
%多行注释
%{ 
xiteP=3;      
xiteI=0.089;     
xiteD=1.5;      
K=1000;
%}

%------------------第三套系数--------------------------% 
%{  
xiteP=1.9;      
xiteI=0.088;     
xiteD=1.9;      
K=500;
%}

%------K越大，系统快速性越好，但增加系统不稳定性-------%
%{  
xiteP=0.001;      
xiteI=0.001;     
xiteD=0.001;      
K=4000;
%}

%初始化 pid 权值
wkp_1=0.10; 
wki_1=0.10; 
wkd_1=0.10; 
error_1=0; 
error_2=0; 
y_1=0;y_2=0;    
u_1=0;u_2=0;    

%ts=0.001;    %采样时间
for k=1:1:500 %采样次数
    
    time(k)=k*ts; 
    r(k)=1;    %阶跃信号
                                                                                                                                                                                                            
    %被控模型
    y(k)=-den(2)*y_1-den(3)*y_2+num(2)*u_1+num(3)*u_2;
    
    error(k) =r(k)-y(k); 
  
    %对学习算法进行规范化处理
    wkp(k)=wkp_1+xiteP*error(k)*u_1*x(1);   %P
    wki(k)=wki_1+xiteI*error(k)*u_1*x(2);   %I
    wkd(k)=wkd_1+xiteD*error(k)*u_1*x(3);   %D 
    
    %比例系数
    x(1)=error(k)-error_1;           %P 
    x(2)=error(k);                   %I 
    x(3)=error(k)-2*error_1+error_2; %D 
    
    wadd(k)=abs(wkp(k))+abs(wki(k))+abs(wkd(k)); 
    w11(k)=wkp(k)/wadd(k); 
    w22(k)=wki(k)/wadd(k); 
    w33(k)=wkd(k)/wadd(k); 
    w=[w11(k),w22(k),w33(k)]; 
    
    u(k)=K*w*x;   % ▲u(k) 控制规律

    %更新数据
    error_2=error_1; 
    error_1=error(k); 
    u_2=u_1;u_1=u(k); 
    y_2=y_1;y_1=y(k); 
    wkp_1=wkp(k); 
    wkd_1=wkd(k); 
    wki_1=wki(k); 
end 

%输出结果
figure(1); 
plot(time,r,'b',time,y,'r'); 
xlabel('time(s)');ylabel('rin,y'); 

%{open 
figure(2); 
plot(time,r-y,'g'); 
xlabel('time(s)');ylabel('error'); 
%}